4. Special Relativity

Vocabulary:

Photon – a particle of light.

The Twins Paradox:

The Twins paradox is a common thought experiment in special relativity. A modified version of this experiment is as follows:

The government wishes to conduct an experiment to prove, once and for all, whether special relativity is true or not. They recruit two twins, Chell and Shell. Chell enters a rocket ship and takes off into space at very fast speed; let it be 90% of the speed of light. Shell does nothing; she just lives normally. As per mission protocol, Chell flies out into space until she runs out of supplies. That is the end of her mission. She then creates a “portal.” This portal links with a portal that Chell made on earth before staring her mission, allowing her to magically return to where she started. After her 17 year mission, Chell steps out of her spaceship and is surprised to find that her sister, Shell, has aged 40 years!

Background:

The twin paradox relies on Einstein’s Theory of Special Relativity. Einstein supposed that the speed of light was constant, regardless of the reference frame of the observer. This result contradicts physical intuition. Using this assumption, he derived a method of relating physics across reference frames. In his 1905 paper, Einstein derived this significant result:

t is the elapsed time in the stationary coordinate system (Shell), τ is the elapsed time in the moving coordinate system (Chell), v is the velocity of the moving system (Chell), and c is the speed of light in a perfect vacuum. Apply this equation for Chell and Shell (i. e. substitute v = 0.9*c, and t = 40) and the twin paradox will appear.

Explanation:

An English translation of Einstein’s 1905 paper is available here. The purpose of this blog post is to present some of the results of the theory in a manner that can be easily understood, while at the same time retaining some faithfulness to the original physics.

A first step in this analysis will be to define a method of measuring time. All choices of units are arbitrary. For example, the English unit, foot, was literally the length of someone’s foot. Similarly, the units of time are arbitrary. For the sake of this analysis, time can then be measured as distance divided by time. For example, moving 10 miles at 10 miles per hour will be 1 hour.

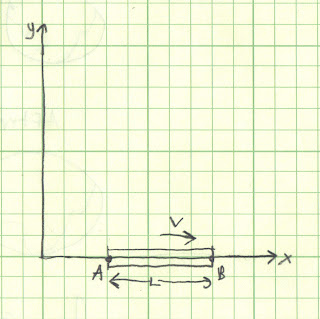
Imagine a rod of length L with endpoints labeled A and B. The rod is oriented as shown in the diagram below; it moves towards the positive x direction with a constant speed v.

You, the observer, are moving next to the rod at with the exact same speed as the rod. Now imagine a photon being released from point A which is heading in the direction of point B. While the photon is moving towards B at speed c, point B is moving away from the photon at the speed v. The net velocity is difference of the two speeds, or c - v. Therefore, the time the photon needs to get from A to B, tAB, is defined:

Now let a photon move from B to A. The photon will move towards A with a speed c, but A is moving towards the photon at a speed v. The net speed will be c + v, and the time, tBA, is

The times are not the same! For all positive values of c and v, tAB will always be greater than tBA. As an illustration of this point, let c = 2 and v = 1, then tAB = L while tBA = 1/3*L. In everyday life, this difference is negligible. The speed of light is approximately 300 million m/s. The fastest commercial airliners move at speeds lower than Mach 1, or 340 m/s. For these values, tAB is only 0.00025 % larger than tBA, an amount so small that it is usually not worth mentioning. All results of special relativity can be derived in manner similar to, albeit more rigorous than, the above analysis.

Results:

We have definitively shown that time is asynchronous when dealing with moving reference frames. This is a central point of The Theory of Special Relativity, and one of the foundations for all of modern physics. Using this example as a starting point, one can begin to develop an intuition for relativistic physics.

References:
[1] A. Einsten, "On the Electodynamics of Moving Bodies."
[2] Wikipedia. Search "Special Relativity"
[3] Wikipedia. Search "Introduction to Special Relativity"

3. Rocket Science

Problem:

How do rockets work?

Background:

In popular culture, the phrases “rocket science” and “brain surgery” are used to represent any task that requires great intelligence or skill. The purpose of this post is to show that rocket science isn’t that hard. You can make rockets too! In addition to this, there are a few common misconceptions which I will clear up.

Solution:

As with most problems in physics, the first place to start is Newton’s laws. Newton’s 2^nd law is commonly stated as force equals mass times acceleration, F = ma. This statement is almost true. The true statement of Newton’s 2^nd is that the change in momentum is related to the force. Momentum is, in turn, the product of mass and velocity. A force can be generated by a change in velocity (acceleration) or a change in mass. The ingenious method employed by rockets is to use a mass change instead of an acceleration change to generate force. This can be illustrated by the example below.

A rocket uses its nozzle to accelerate the flow at exit to a high speed above the inlet velocity. Due to the shape of the nozzle the speed at exist must necessarily be higher than the speed at the inlet. (See solution section of this post for the proof.) Applying Newton’s 2^nd law to a fluid element and making simplifying assumptions relevant to this problem, we can derive this equation

F = mt*v +p*A (Equation 1)

Where mt, is the mass flow rate. It represents the rate at which the rocket is losing mass. The net momentum flux, mt*v, results in a force on the rocket (thrust) which accelerates the rocket forward. In addition, the pressure causes a force on the rocket which is proportional to the nozzle area. There is a common misconception that the pressure at the nozzle exit causes thrust. The equation demonstrates that the fluid flux, alone, is enough to produce force in the rocket.

Model Limitations:

A major limitation with the usefulness of Equation 1 is lack of information. It would be very difficult or impossible to know all of the values for velocity and pressure. However, given this information, the force can be calculated exactly.